Cartel Problems
Even if cartels were legal, theory suggests we wouldn’t expect them to last very long:
Entry Problems → Excess profits for the cartel will induce firms to join the market
Cartel Cheating → Incentive for firms in the cartel agreement to deviate and earn significantly higher profits
Unequal Costs → Most firms don’t have the same cost to produce
Entry Problems
Free entry
- In order for a cartel to be effective, it must be protected with entry to barrier.
- Otherwise, new entrants will serve as the competing force and undermine the cartel’s efforts to increase price.
- Excess profits shared by a cartel may attract large-scale entry, causing the agreed-upon cartel quantity level to become excess capacity. This, in turn, makes the collusive agreement less effective.
- In the real world, cartels can deter entry through a variety of avenues
- Patents: a company that controls a patent can dictate who is allowed to enter a market and who is not
- Licensing: forcing entrants to acquire an official permit to operate in an industry (e.g. taxis, liquor stores)
- Owning an essential input: if an entrant has no access to an essential facility in the production of the good, they cannot enter the market (e.g. OPEC)
Infinite number of identical firms
- In building our model, we assumed there were an infinite number of potential entrants to the market, who all had access to the same technology (i.e. all had the same cost functions)
- A cartel could exist if its members were all more efficient than the potential entrants (e.g. shared technology, experience, inside information)
- Since these firms are more efficient, raising the price induces only a limited number of firms to enter the market
Cartel Cheating
- As we’ve discussed, members of a cartel have incentive to cheat
- Claim: if everyone else is “playing fair” then a single firm can benefit by expanding their output (at the expense of the cartel)
- Suppose there exist 100 firms in an industry where total industry demand is \(Q = 1000 - 2P\)
- Suppose each firm gets an equal share of the industry: \[ \begin{aligned} q&=\frac{Q}{100} \\ &= \frac{1000}{100} - \frac{2}{100}P \\ &= 10-\frac{1}{50}P \end{aligned} \]
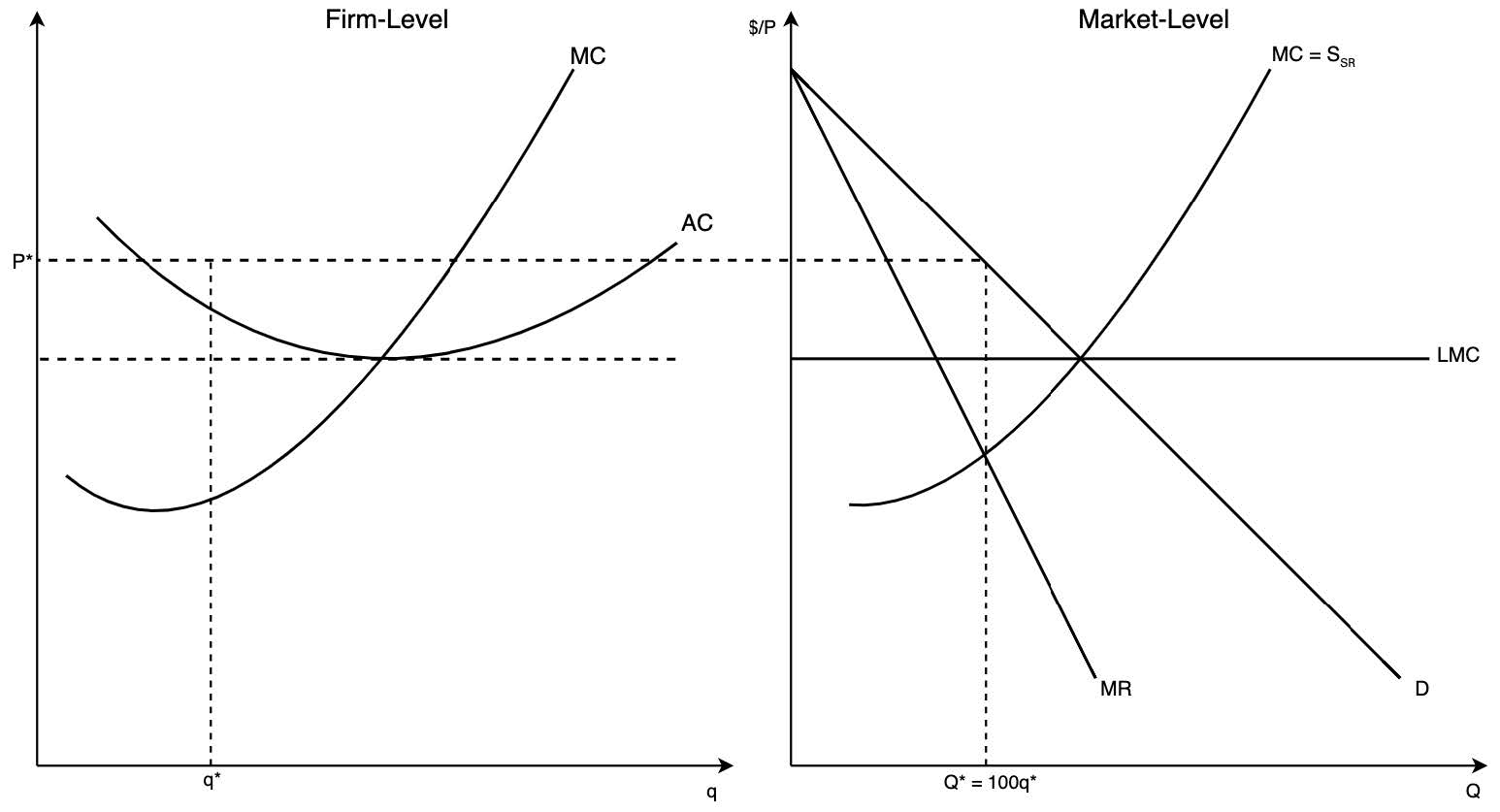
- The cartel is maximizing profits when total output is at Q* = 100q*
- Each member must agree to produce q*
- The price associated with this level of output is P*
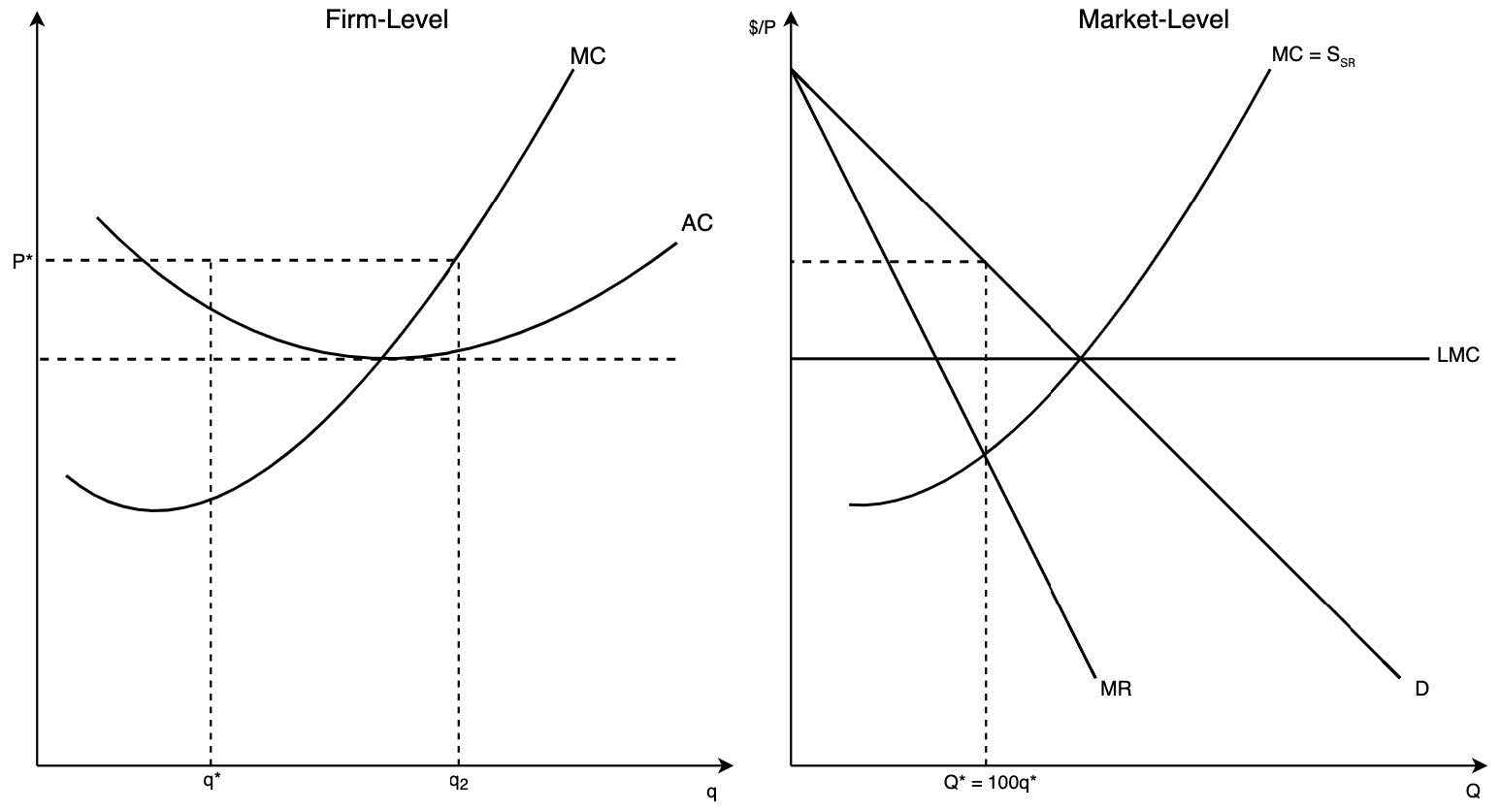
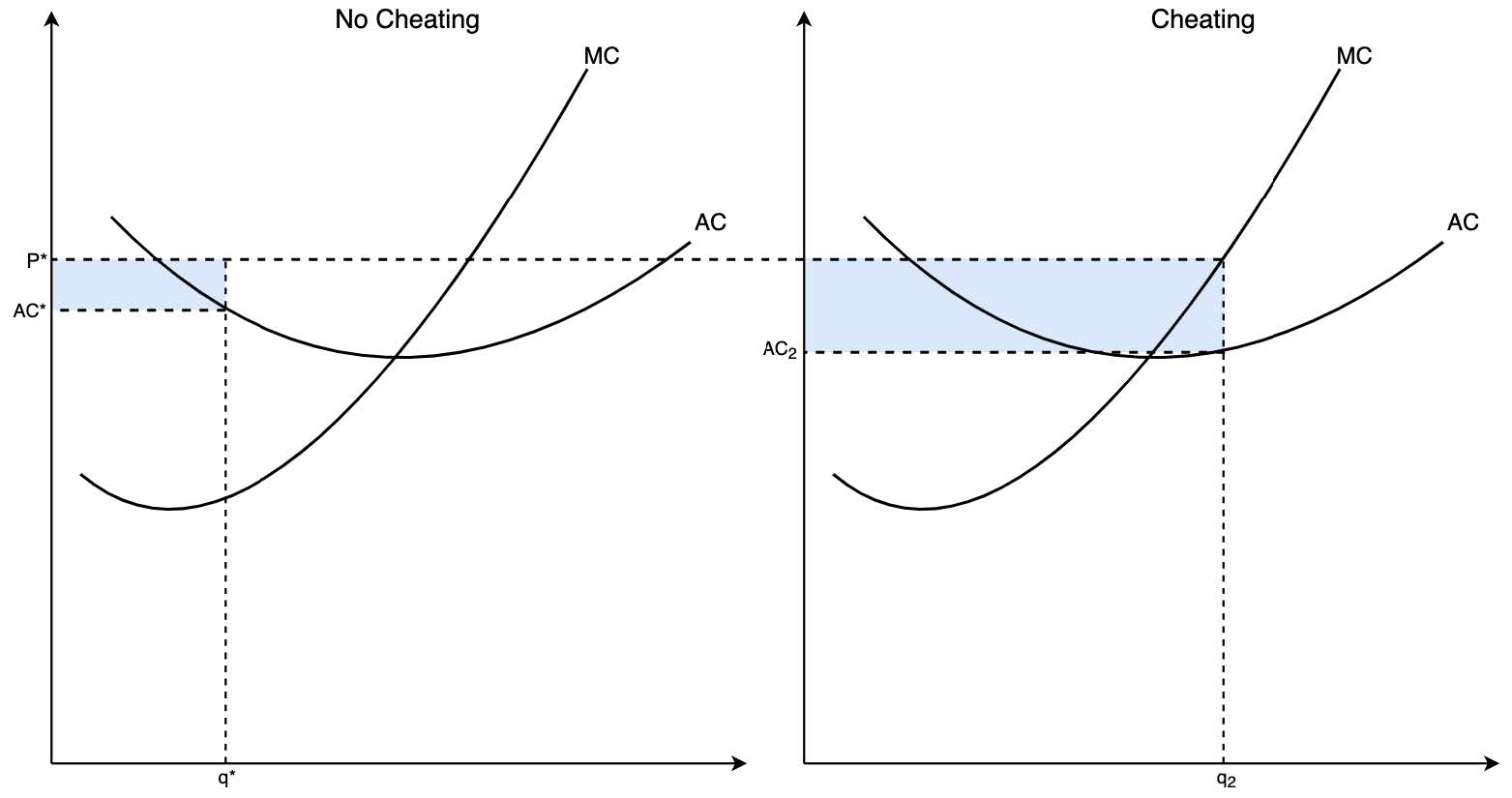
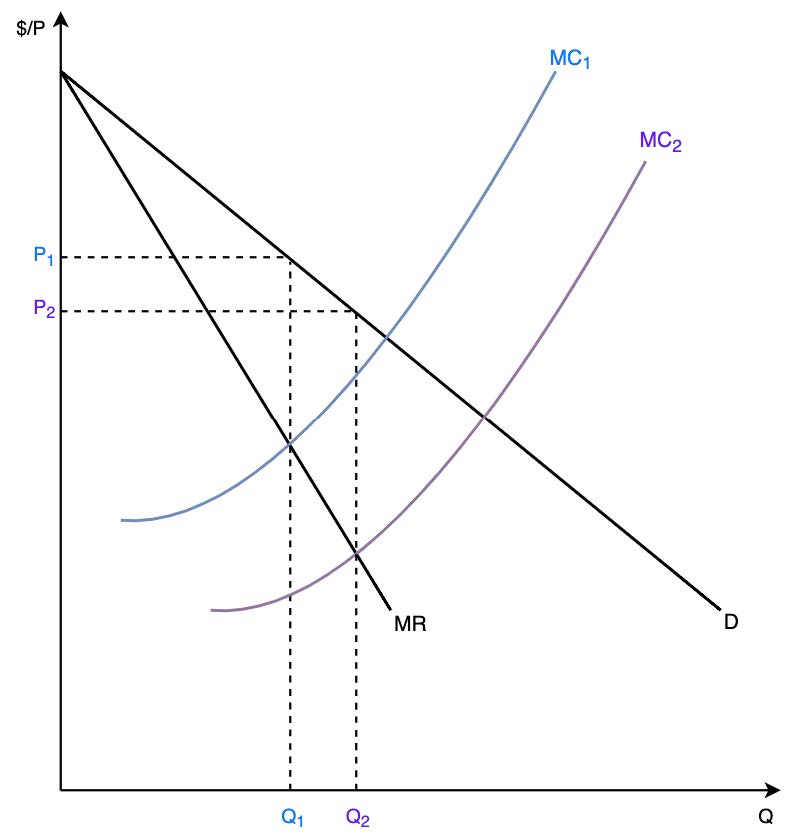
- Indiviudal firm has incentive to produce more given the cartel price assuming that no other members of the cartel cheat
- But all members of the cartel will face similar temptations, yielding total industry output to expand significantly beyond \(Q^*\) and price to plummet to the competitive level
- Each firm has incentive to deviate from the agreed amount to enjoy unexploited economies of scale and higher profits generated from the fixed price, assuming no one else cheats
- This benefits the individual firm a lot but impacts optimality for the rest of the cartel
- Cartel will eventually fall apart
Numerical Example1
Suppose there are only two firms, A and B. Suppose they produce the same product and have identical cost of production.
Given market demand, will these two firms collude?
Suppose that market demand is given by: \[ P = 100-q_A - q_B \]
If each firm maximizes its profits by acting competitively without collusion,
- Firm A’s MR: \(MR_A = 100-2q_A - q_B\)
- Firm B’s MR: \(MR_B = 100-q_A - 2q_B\)
- Suppose firm A and firm B’s marginal cost and average total cost are all equal to 20
Finding the equilibrium output for each firm, \[ \begin{aligned} q_A^*&=80/3 \\ q_B^*&=80/3 \\ P^* &= 140/3 \end{aligned} \]
Finding each firm’s equilibrium profit, \[ \begin{aligned} \Pi_A^*&=711.11 \\ \Pi_B^*&=711.11 \end{aligned} \]
If the two firms collude and produce quantity that jointly maximize the profit,
- MR: \(MR = 100-2q\)
- Suppose firm A and firm B’s marginal cost and average total cost are all equal to 20
Finding the equilibrium industry output, price and each firm’s output, \[ \begin{aligned} q^*&=40 \\ P^*&=60 \\ q_A^*&=40/2 = 20 \\ q_B^*&=40/2 =20 \\ \end{aligned} \]
Finding each firm’s equilibrium profit, \[ \begin{aligned} \Pi_A^*&=800 \\ \Pi_B^*&=800 \end{aligned} \]
Now suppose firm A decides to increase its output slightly from 20 to 80/3 (profit maximizing quantity). This will change the market price since more output is supplied to the market. If firm B continues to produce the colluded amount, 20 units, then \[ P = 100- (80/3)-20 = 160/3 \]
Finding each firm’s equilibrium profit, \[ \begin{aligned} \Pi_A^*&=(\frac{160}{3}-20)\frac{80}{3} = 888.89\\ \Pi_B^*&=(\frac{160}{3}-20)20=666.67 \end{aligned} \]
This means that each firm has incentive to cheat and produce more than the agreed amount, at the expense of the other colluder. Once firm B realizes that firm A cheated, firm B will also deviate from the agreement and produce more. This eventually unravels the cartel.
Punishment
- Punishing cheaters is hard
- As consumers, we have no problem with punishment
- Cartels are illegal so they can’t ask for legal help
- Fighting back against cheaters usually means lowering prices which hurts cartels even more
- Thus, maintaining a cartel relies on deterring cheating
- To discuss deterrence, we need to think about cartel activities in a dynamic format (i.e. repeated game)
- Let’s express the cartel decision as a dynamic game
- Every period, a member of the cartel can choose to listen to the cartel “steering committee” or they can cheat
- Each member knows each firms strategy in the previous period (i.e. did other firms cheat or comply?)
- Every firm is trying to maximize their present value of profit
- This setup incentivizes firms to employ a trigger strategy
- A single firm can deviate from the cartel agreement and potentially make much more profit in a single period
- However, after that period, all other firms retaliate and act competitively for the rest of the time, eliminating any future cartel profits
Trigger strategies
Present Value of Profits From Cooperating
If the firm cooperates, they will make some profit forever (specifically, their portion of the cartel profit)
Let r be the discount rate for future profits and \(\Pi^*\) be the profits that would result from cooperating with the cartel \[ \begin{aligned} PV(\text{cooperate}) &= \Pi^* + \frac{\Pi^*}{(1+r)}+ \frac{\Pi^*}{(1+r)^2}+ \cdots \\ &= \sum_{t=0}^{\infty} \frac{\Pi^*}{(1+r)^t} \\ & =\sum_{t=0}^{\infty}\Pi^*\beta^t \\ &=\frac{\Pi^*}{1-\beta} \end{aligned} \]
Present Value of Profits From Cheating
For these problems, we’re assuming that firms have a trigger strategy where they will act competitively if any firm cheats in the previous period
We’re assuming that this will lead to zero profits (long-run competitive equilibrium) so a firm that cheats will only earn profit in the period that they cheat.
Again, let r be the discount rate over future profits and let \(\Pi_{\text{cheat}}\) be the profits a firm can earn from cheating
\[ \begin{aligned} PV(\text{cheat}) &= \Pi_{\text{cheat}} + \frac{0}{(1+r)} + \frac{0}{(1+r)^2} + \cdots \\ &= \Pi_{\text{cheat}} \end{aligned} \]
Hence, the present value of all future profits from cheating is only equal to the profits they earn in the period the cheating occurs.
Trigger Strategies Example
Assume the following:
- r = 0.25
- Profits from cooperating is $200,000
- Profits from cheating are $750,000
First find \(\beta\) using the discount rate: \[ \beta = \frac{1}{(1+r)} = \frac{1}{1.25} = 0.8 \]
Now plut in values to get the present values to get the present value of all future profits when cooperating: \[ \begin{aligned} PV(\text{cooperate}) &= \frac{\Pi^*}{1-\beta} \\ &= \frac{200000}{1-0.8} \\ &= 1,000,000 \end{aligned} \]
The firm will find it optimal to cooperate; the trigger strategy worked
\[ 1000000 > 750000=PV(\text{cheat}) \]
Barry Haworth homepage(https://econpage.com/301/handouts/Cartel/cartel.html)↩︎