Monopolist’s profit maximization
Simple example
Profit maximization, regardless of market power, always occurs where marginal revenue equals marginal costs
\[ MR=MC \]
The defining feature of a monopoly is that they are the only supplier in the market. This implies they are a price-setter. Demand reacts to the price chosen by the monopolist
\[MR\neq P\]
Hence, the marginal revenue function (and total revenue function) for a monopolist is different than that of a perfectly competitive firm:
\[ TR(q)=p(q)\cdot q \\ MR(q)=p'(q)\cdot q + p(q), \]
- where \(p(q)\) is the maximum price the market will pay if \(q\) units were put up for sale,
- \(p(q)\) is referred to as the inverse demand function.
Profit maximization by a monopolist follows the basic process:
- Find \(q_m\) such that \(MR=MC\)
- Set price \(p_m= p (q_m)\)
Suppose inverse demand and total cost for a monopolist are given by the following functions:
\[ \begin{aligned} p(q)&=100-q\\ TC(q)&=100+q^2 \end{aligned} \]
Then the total revenue function can be found as such:
\[ \begin{aligned} TR(q) &=p(q)\cdot q \\ &=100q-q^2 \end{aligned} \]
Important Trick → with a linear demand function, the marginal revenue function for a monopolist always has the same intercept as demand with twice the slope
\[ MR(q)=100-2q \]
Now we’re ready to solve for the profit maximizing price and level of output for the monopolist:
\[ \begin{aligned} MR(q) &=MC(q)\\ 100-2q &=2q \\ 100 &=4q \\ 25 &=q_m \end{aligned} \]
After finding the profit maximizing quantity, we plug \(q_m\) into the inverse demand equation to find the price consumers are willing to pay:
\[ p(q_m=25) = 100-25=75 \]
Another example with implications
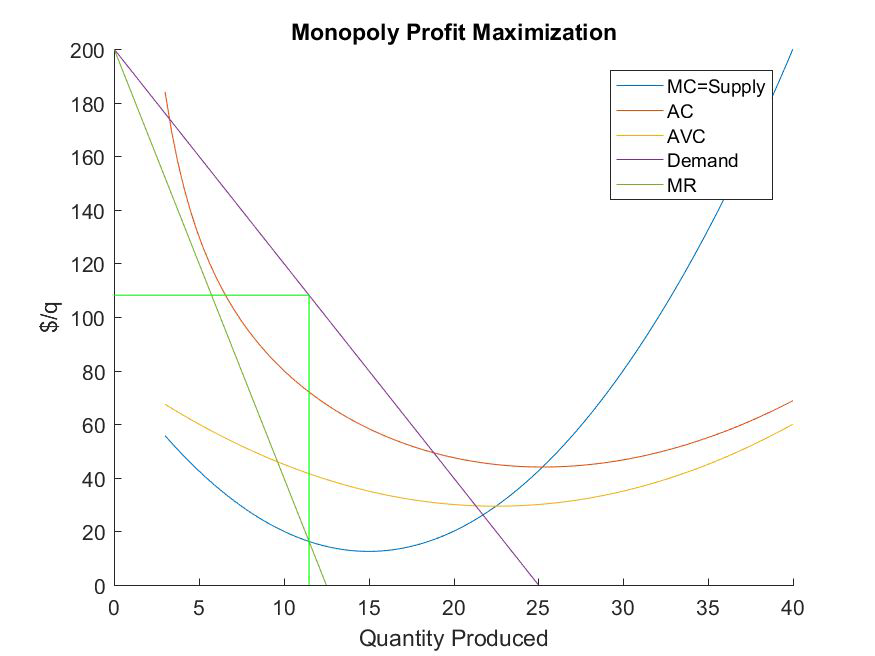
The profit maximizing level of output is the quantity that equates marginal revenue and marginal cost:
- Firms then exploit their market power by pricing according to the consumers’ maximum willingness to pay at that quantity
- Graphically, at the profit maximizing quantity, firms move up to the demand curve to set the price
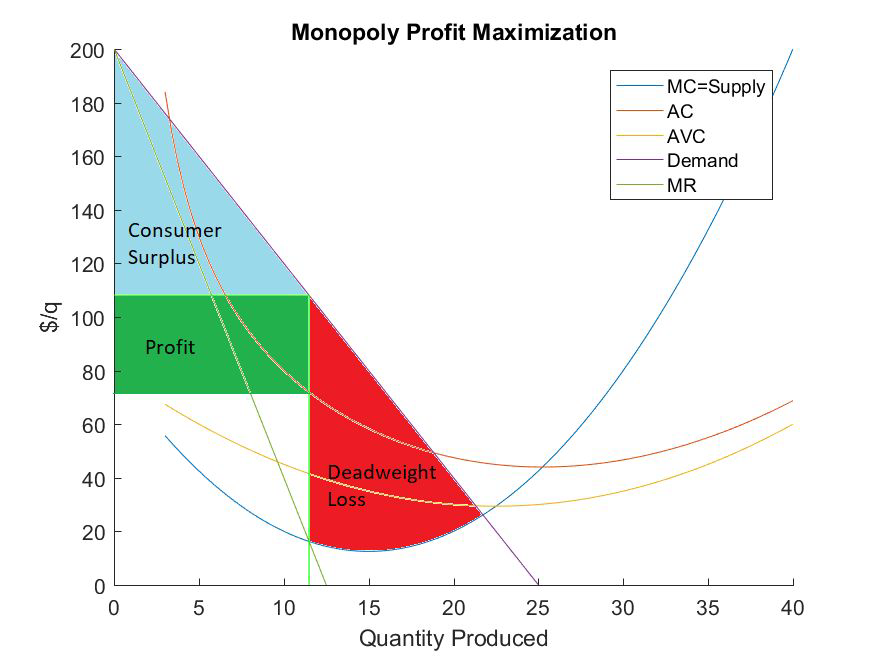
- The result is a lot of deadweight loss!
- From a social welfare perspective, this outcome is economically inefficient.